

“b” is positive, zero, or negative, depending on whether, as the independent variable increases, the value of dependent variable is predicted to increase (panels i and ii), remain unchanged (iii), or decrease (iv). “b” represents predicted change in the value of dependent variable (on Y axis) for each one unit increase in the value of independent variable (on X axis). Relationships between two quantitative variables and their regression coefficients (“b”). Furthermore, the higher the magnitude of “b,” the steeper is the change in Y with change in x. If the value of Y does not change with x, the value of “b” would be expected to be 0. The value of “b” is positive when the value of Y increases with each unit increase in x and is negative if the value of Y decreases with each unit increase in x. It is also referred to as “coefficient,” “regression coefficient,” or “gradient.” Note that lowercase letters (x and y) are used to denote the actual values and capital letters (Y) for predicted values. Where “x” is the known value of independent (or predictor or explanatory) variable, “Y” is the predicted (or fitted) value of “y” (dependent, outcome, or response variable) for the given value of “x”, “a” is called as the “intercept” of the estimated line and represents the value of Y when x = 0, and “b” is called as the “slope” of the estimated line and represents the amount by which Y changes on average as “x” increases by one unit. Intercept is shown as “a” and slope or regression coefficient as “b” The capital letters (Y) are used to indicate predicted values and lowercase letters (x and y) for known values. Each dot corresponds to a data point, i.e., an individual pair of values for x and y, and the vertical dashed lines from each dot represent residuals. This is done using “multiple linear regression.” We will not discuss this more complex form of regression.Īlthough the concepts of “correlation” and “linear regression” are somewhat related and share some assumptions, these also have some important differences, as we discuss later in this piece.ĭata from a sample and estimated linear regression line for these data. For instance, one study found that whole-body fat content in men could be predicted using information on thigh circumference, triceps and thigh skinfold thickness, biceps muscle thickness, weight, and height. The independent and dependent variables are, by convention, referred to as “x” and “y” and are plotted on horizontal and vertical axes, respectively.Īt times, one is interested in predicting the value of a numerical response variable based on the values of more than one numeric predictors. This can be done using “simple linear regression” analysis, also sometimes referred to as “linear regression.” The variable whose value is known (MUAC here) is referred to as the independent (or predictor or explanatory) variable, and the variable whose value is being predicted (BMI here) is referred to as the dependent (or outcome or response) variable.
As a next step, they may be tempted to ask whether, knowing the value of one variable (MUAC), it is possible to predict the value of the other variable (BMI) in the study group. If the dots fall roughly along a straight line, sloping either upwards or downwards, they would conclude that a relationship exists. In such a situation, as we discussed in a recent piece on “Correlation” in this series, the researchers would plot the data on a scatter diagram. For instance, in a recent study, researchers had data on body mass index (BMI) and mid-upper arm circumference (MUAC) on 1373 hospitalized patients, and they decided to determine whether there was a relationship between BMI and MUAC.
values of one characteristic vary depending on the values of the other.
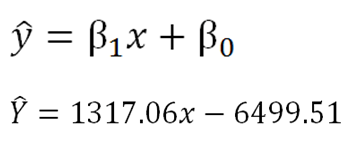
We often have information on two numeric characteristics for each member of a group and believe that these are related to each other – i.e.


 0 kommentar(er)
0 kommentar(er)
